| SINCE 10 MAR 2008 | |||||||||||||||||||||||||||
| HOME |
|
||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||
 ある島に発生したカルマンの渦列 (NASAのホームページより) |
|||||||||||||||||||||||||||
|
流体中で運動する物体(ウキ)には、粘性に基づく摩擦による「せん断応力」が働き、進行方向の反対側(後方)に渦流が発生し、運動エネルギーに大きな損失を与えます。流体摩擦は境界層内の流れと、固体表面(凸凹であるより滑らかが良いと言うことなので説明は省略します)の状態によって決定されるので、エネルギーの損失を回避するには、物体表面を滑らかにすることが簡単且つ有効な手段と言えます。 しかし、前述のディンプルを施したゴルフ・ボールは、表面が決して滑らかではありません。故意に凸凹が施されています。にも拘わらず、空気抵抗が軽減され、飛距離を伸ばすことに成功しています。これは何故でしょうか? ゴルフ・ボールは高速で回転しながら、小さな乱流を境界層内に多数発生させます。乱流を発生させることで、境界層の剥離地点を後部へ移動さています。つまり、エネルギーの損失を招く境界層の剥離には、粘性に基づくせん断応力が必ず伴いますし、流体の粘性は変えられませんので、境界層内の流れに変化をつけ、渦流の影響を受ける面積を極力小さくするアイデアを考えた訳です。これが見事に成功し、今では全てのゴルフ・ボールに、あの凸凹があります。一見空気抵抗を増加させそうなあの凹みも、実は流体力学の理論が大いに役に立っていた訳です。 ゴルフ・ボールでディンプルが成功したからと、単純にそれをウキに導入するのは余りにも短絡過ぎます。低粘度、高圧縮の気体中でこそ可能なのであって、高粘度、低圧縮の水が相手ではそうは行きません。ディンプルはいたずらに表面積を増やし、流体摩擦(粘性摩擦)の増加を招くだけです。ウキにとってディンプルは逆効果です。 ●ゴルフ・ボールのディンプルに関する情報はこちらをご覧下さい。→「ゴルフボールのディンプル数」(PDFです。 |
|||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||
|
「アルキメデスの原理」は誰しもが必ず習う物理の基本理論です。今更らですが、流体の単位体積の重さをγ、物体により排除された流体の重さをV、とすると浮力Bは、B=γVとなります。即ち「流体中の物体は、その浮力の大きさに等しいだけ、見かけの重量を減ずる。」と言う真理がアルキメデスの原理です。 今では小学生でも知る理論ですが、当時としては革新的であったこの理論も、風呂桶の水が溢れ出すのをヒントにして生まれました。ウキに関する新しい理論が、自宅の風呂桶から生まれても何ら不思議はありません。 |
|||||||||||||||||||||||||||
 アルキメデス Archimedes 紀元前287年~212年 シチリア生まれの数学者 |
|||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||
 円錐ウキ |
|||||||||||||||||||||||||||
|
「流体中の物体はその浮力の大きさに等しいだけ見かけの重量を減ずる」と言う原理から、流体中の物体により排除された流体の重心を「浮力の中心」または「浮力の作用点」と呼び、船舶の設計に於いては大変重要な意味を持ちます。何段にも詰まれたコンテナを運ぶ輸送船の安定性は、正にこの「浮力の中心」を基本に求められ、限界ギリギリまでコンテナを積み安全に航海できるようになる訳です。 この「浮力の中心」は当然ウキに於いても大切な要素で、「ウキの安定性と復元性」を考える上で大いに参考になります。下の【図-4】【図-5】は流体中に浮揚する物体の状態を表わします。 |
|||||||||||||||||||||||||||
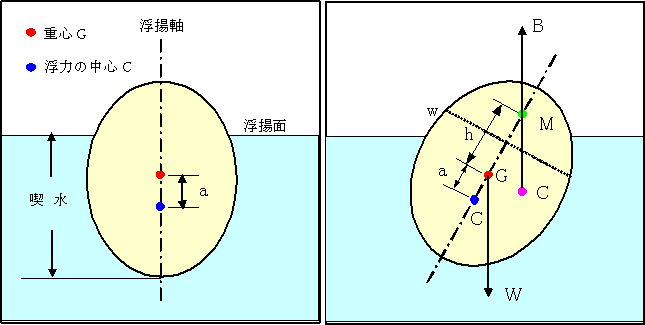
【図-4・5】浮揚軸・浮揚面・浮面心・喫水並びにメタセンタ |
|||||||||||||||||||||||||||
| 【図-4・5】で、物体の重量をW、浮力をBとすると、他に力が作用しないと仮定すると、物体はW>Bで沈下し、逆にW<Bで浮上します。またWとBが同一線上にない場合は回転します。 従って、浮揚して静止する物体の浮力は、その物体の圧力により排除された流体の重量に等しく、その「作用線」は物体の中心を貫くことになります。物体の重心Gと、浮力の中心を貫く鉛直線(糸に鉛を吊るした際にできる直線)を浮揚軸と呼び、浮揚面とは浮揚する物体の水面による切断面を指します。更に、浮面心とは浮揚面の中心を指し、喫水は浮揚面から物体の最下部までの距離を指します。 また、【図-4】のように安定して浮揚する物体を【図-5】のように傾けると、新たに移動した浮力の作用線と浮揚軸とが交わります。この交わった点をメタセンタと呼びMで表わします。そしてメタセンタの高さとは重心からメタセンタの長さhを指します。 浮揚体はメタセンタMが重心Gの上にあり、重さWと浮力Bとが吊り合っている場合は安定します。逆にメタセンタが重心の下方にある場合は不安定になります。 これらの事実は、目的とするウキを自立式にするか、しないかの良い判断材料になります。 |
|||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||
|
下の【図-6】は、同一断面積を有する円柱の抵抗係数を示したものです。この際、両端の形状を無視して、太さが同じで長さの異なる棒浮きだと考えて数値を見て下さい。 |
|||||||||||||||||||||||||||
図-6】 同一断面積の三次元物体の抵抗係数 |
|||||||||||||||||||||||||||
| 【図-6】は橋脚、水門の格子、鉄鋼構造物の間を吹き抜ける風の影響等の計算に用いらる三次元物体の抵抗係数です。実に興味深いのは、4本の円柱は皆同一の断面積を持ち、一様に同じ流れの中に置かれて計測されます。しかし、比率1:1の円柱は、体積でその2倍ある1:2の円柱より抵抗値が高く、また比率1:4の円柱では、体積がその4倍あるのに抵抗係数は0.87です。更に、比率1:7に至っては、その体積が7倍にも拘わらず、抵抗値は0.99です。そして比率1:7で初めて比率1:1の抵抗値を僅かながら上回ります。 実験によりもたらされた結果から、比率1:1の円柱は、流れの後方に発生する渦流の影響を受けやすい形状(比率)だと結論付けられます。これは境界層の剥離が他の比率の円柱より前方向で発生する為と考えられます。比率が1:7を超えると、抵抗値は比例して増大します。これらの事実はウキの持つ断面積と長さを考える上で大変参考になります。下の【図-7】は平行な流れの中に置かれた円柱の後方に発生する渦流の様子です。 尚、これは円柱が完全に水中に没していることを前提にしています。実際には水中にあるウキは目視できませんので、ウキはそのトップだけでも露出している必要があります。 |
|||||||||||||||||||||||||||
 【図-7】 円柱後方に発生した渦流の様子 |
|||||||||||||||||||||||||||
| 三次元物体の形状は、理論的には無限に存在します。当然異なる形状の三次元物体の抵抗値の計測も無限に存在します。しかしながら、如何に抵抗を効率良く軽減させるるかを考えるウキの世界では、抵抗係数の増加する形状に関する研究は、当然除外されますし、何の意味も持ちません。ウキに使用可能な形状は限られています。それが繊細であれば有るほど選択肢は減って行き、自ずとその全体像が見えてきます。 下の【図-8】は【図-6】と同様に、流体中での同一断面積で長さの異なる円柱の抵抗係数です。これは【図-6】とは異なり、横からの一様な流れに対するもので、ウキの潮の流れに対する性能を推定することが出来ます。所謂「潮に乗り易いウキ」です。 |
|||||||||||||||||||||||||||
【図-8】 同一断面積の三次元物体の抵抗係数 |
|||||||||||||||||||||||||||
| ここまでの幾つかの流体力学上の実験成果から、おぼろげに求めるウキの基本的要件は見えてきた筈です。特に大切なのが流れの後部方向に発生する「渦流と境界層の剥離」でしょう。 渦流により流体中の物体は、進行方向とは逆の力を受け、エネルギーの損失を招きます。これはウキの「慣性運動」にも大きく影響し、「エネルギー保存能力」が著しく削がれる結果となります。また、三次元物体の流体中で示す抵抗係数の数値は、更に驚きだと思います。専門家には当たり前なことでも、一般の人には新鮮で楽しいものです。 これらの流体力学上の数値や結果は、ウキを研究する上では欠かせないものばかりです。ウキとは全く関係ない世界でも、世の中を眺めるのに大いに役に立つ筈です。「河はなぜ蛇行しながら流れるのか」から始まり、イロイロと異なって視点からものを見つめ、数々の新しい発見が必ずできます。 専門の学者を目指すのでなければ、難しいことを多く知る必要はありません(?)。簡単なことでも知れば知るほど面白くなります。「求めることは知ること」です。「知ることは違った視点で考えられる」ことです。人それぞれレベルが異なりますが「学問する」ことは実に楽しいものです。 |
|||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||
|
高速で泳ぐカツオやマグロなどの魚は、どれも例外なく流線型の体型をし、魚体は鱗(ウロコ)も無く滑らかです。それはその体型と体表が高速移動するのに適しているからに他なりません。 身近な金魚でも、「流金」のようにヒラヒラと優雅に泳ぐものと、「和金」のようにすばやく泳ぐものとでは、体型に明らかな違いが見られ、その鰭(ヒレ)の形や硬さもも大きく異なります。説明に丁度良い写真が有りません(以前は持っていたのですが残念ながら行方知れずです)が、「流金」は泳ぐ際に発生した渦流が魚体に纏わり付いた状態になり、一方、より原型のフナに近い「和金」では、渦流が尾びれから後方にかけて発生し、明らかな運動能力の違いを見せます。これは「境界層の剥離と流体摩擦」とで述べた通り、粘性を持った流体が固体表面に沿って流れ、その速度が下流に向かって増加する場合、その圧力は固定表面に於いて下流うに向かって下降します。逆に下流に向かって速度が下降すると、圧力は増加します。このことから解る通り、高速で泳ぐ「和金」はより高速が出せる体型をし、人工的に作り出された「流金」はその必要が無いので、丸いデブった体型をしています。 勿論、ウキとは異なり、金魚にとって粘性抵抗(粘性摩擦・流体摩擦)は、体をくねらせることで前進するエネルギーを得るのに、無くてはならない原動力となります。自らが運動する魚類と、他力で沈降するウキでは、粘性摩擦の意味も、またその価値も異なります。ウキにとって粘性摩擦は邪魔者以外の何者でもありませんが、金魚にとっては欠かすことのできない大切な原動力と言えます。 |
|||||||||||||||||||||||||||

|
|||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||
|
球体は三次元物体中、同一表面積では最小の体積を持ち、同一体積では最小の表面積を持つと言う極めて特徴的な一面があります。また球体は表面が滑らかな曲線で構成され、一切の凹凸が有りません。更に注目すべきは、滑らかな曲線で構成される三次元物体は、全て球体を引き伸ばした延長線上に位置することです。 流体中を運動する物体は、その固体表面と流体の粘性に基づくせん断応力が働き、境界層の剥離現象が起き、流れの後方に渦流が生じます。この渦流は条件によっては規則正しい場合も有るし、また乱流になる場合も有ります。規則正しい渦流をカルマンの渦烈と呼び、レイノルズ数60~5000の場合に出現します。渦列が安定するにはb/a=0.2806の場合に限られ、この時渦烈は互いに影響しあい、誘導しあって進行します。【図-9】 |
|||||||||||||||||||||||||||
 【図-9】 規則正しいカルマン渦列 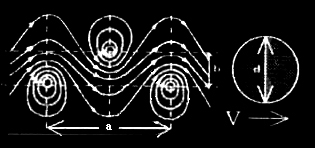 【図-10】 カルマン渦列の図解 |
|||||||||||||||||||||||||||
| 球体は低速では粘性摩擦に基づくせん断応力が働き、大きな抵抗が生まれます。速度を上げレイノルズ数のやや高い範囲では、速度の2倍に比例して抵抗値が上昇します。更に速度を上げ境界層の剥離から乱流剥離まで進むと、抵抗値が激減[Reが(1.5~4)×105程度]する箇所があります。突然抵抗が減る訳です。その後速度を上げると、また抵抗値は上昇します。 大変面白い現象ですが、高速で圧縮性の高い流体中を移動する場合ですので、ウキには無縁のことですが書いてみました。。 一方、粘性抵抗の高い水槽実験では、大変面白い特徴的な運動能力も示します。浮力をやや上回るオモリを負荷すると、静かに沈降しますが、負荷を徐々に増加させると、激しく振動しながら沈降します。これは発生した後部渦流の影響をまともに受けるからと考えられます。しかし流体と同比重(サスペンド状態)の験体では、小さい瞬間負荷にも確実に反応し、静かに、そしてゆっくりとゆっくりと沈降します。それはまるでスローモーションの動画を見ているかの錯覚に襲われます。恐ろしく緩慢な速度で、他の験体の数倍の時間をかけ沈降します。 実に面白い結果です。実験してみて始めて判る球体の特徴的な一面です。この現象は、遅い速度では境界層が剥離するまでに至らず、固体表面に発生した小さな乱流がまとわり着き、これが球体の後部に回りこみ、球体を押し下げるエネルギーになっていると想像できます。ある意味(ある時点)では慣性運動能力が高い(?)とも言える面白い現象です。下は試作した球体ウキで実際に釣行テストも行いました。 |
|||||||||||||||||||||||||||

|
|||||||||||||||||||||||||||
 Traditional Japanese colors |
|||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||